다익스트라 알고리즘(Dijkstra Algorithm)
다익스트라 알고리즘은 그래프의 한 정점에서 다른 정점으로의 최단 경로를 찾기 위해 사용되는 최단 경로 알고리즘입니다. 최단 경로를 찾는 알고리즘 하면 BFS를 떠올릴 수도 있지만, 다익스트라는 BFS(넓이 우선 탐색) 알고리즘과는 다르게 가중치가 존재하는 그래프에서 최단 경로를 찾을 때 사용됩니다. 이 때 그래프의 가중치는 음수가 될 수 없습니다.
특정 노드에서 각 노드까지의 최단 경로를 찾기 위해 사용하는 알고리즘인 만큼 실생활의 활용 예시로는

1. 지도의 특정 지점에서 다른 지점까지의 최단 경로 찾기
2. 컴퓨터 네트워크에서의 데이터 패킷의 최적 경로를 찾기 위한 네트워크 라우팅
등 에서 사용됩니다.
다익스트라 알고리즘 구현
다익스트라 알고리즘의 핵심은 현재 노드와 연결된 노드를 모두 탐색하면서 최소 이동 비용을 매번 갱신해 주는 것입니다. 이해하기 쉽게 그림과 과정을 통해 다익스트라 알고리즘의 구현 과정을 알아봅시다.
1. 최단 거리의 기준이 되는 시작 노드(노드 S라고 합시다)를 선정합니다. 이 때 시작 노드는 방문처리를 합니다.
2. 노드 S 기준으로 각 노드까지의 최단거리를 저장합니다.
3. 방문하지 않은 노드 중 가장 비용이 적은 노드(노드 N이라고 합시다)를 선택합니다.
4. 노드 N과 연결된 노드의 최단 거리를 모두 갱신해 줍니다(기존 연결 노드의 최단거리와 노드 N까지의 최단거리 + 연결 노드까지의 거리를 비교)
5. 모든 노드를 방문할 때까지 3번과 4번 과정을 반복합니다.
아래와 같은 4개의 노드로 이루어진 그래프가 있다고 가정해 봅시다.

시작 노드를 1로 설정하고 방문처리 후 노드 1과 연결된 노드들의 거리를 설정해 줍니다.

방문처리한 노드 1과 연결된 미방문 노드 중 거리 비용이 가장 작은 노드를 방문 처리 후 해당 노드와 연결된 노드들의 최단 거리를 갱신합니다. 기존 최단 거리와 현재 노드의 최단 거리 + 현재 노드와 연결 노드 사이의 거리를 비교하여 더 작은 비용으로 갱신합니다.
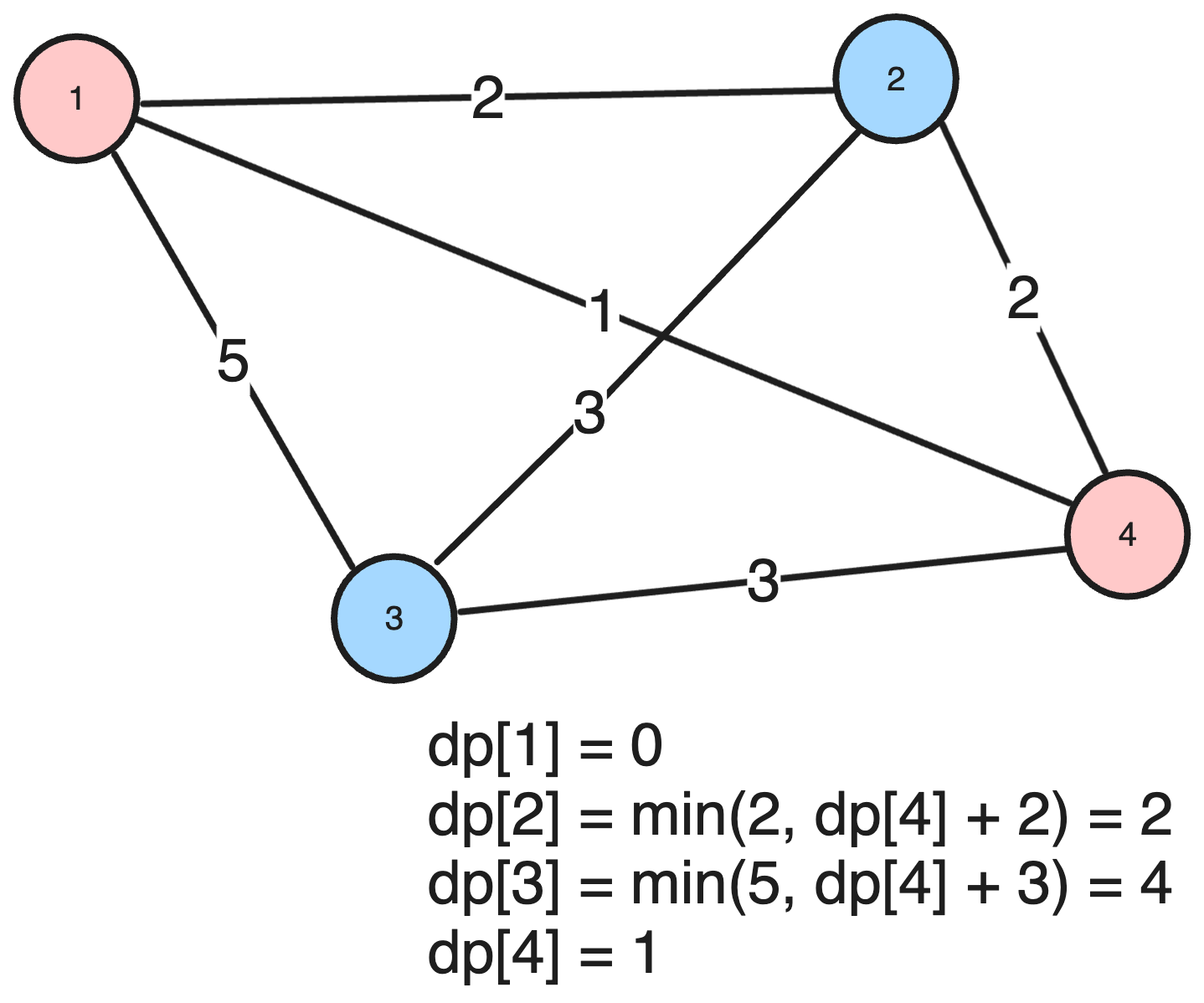
같은 방법으로 노드 2, 노드 3도 갱신 처리를 해주면 결과가 나옵니다. 시작 노드 1에서 각 노드까지의 최단거리는 아래와 같습니다.
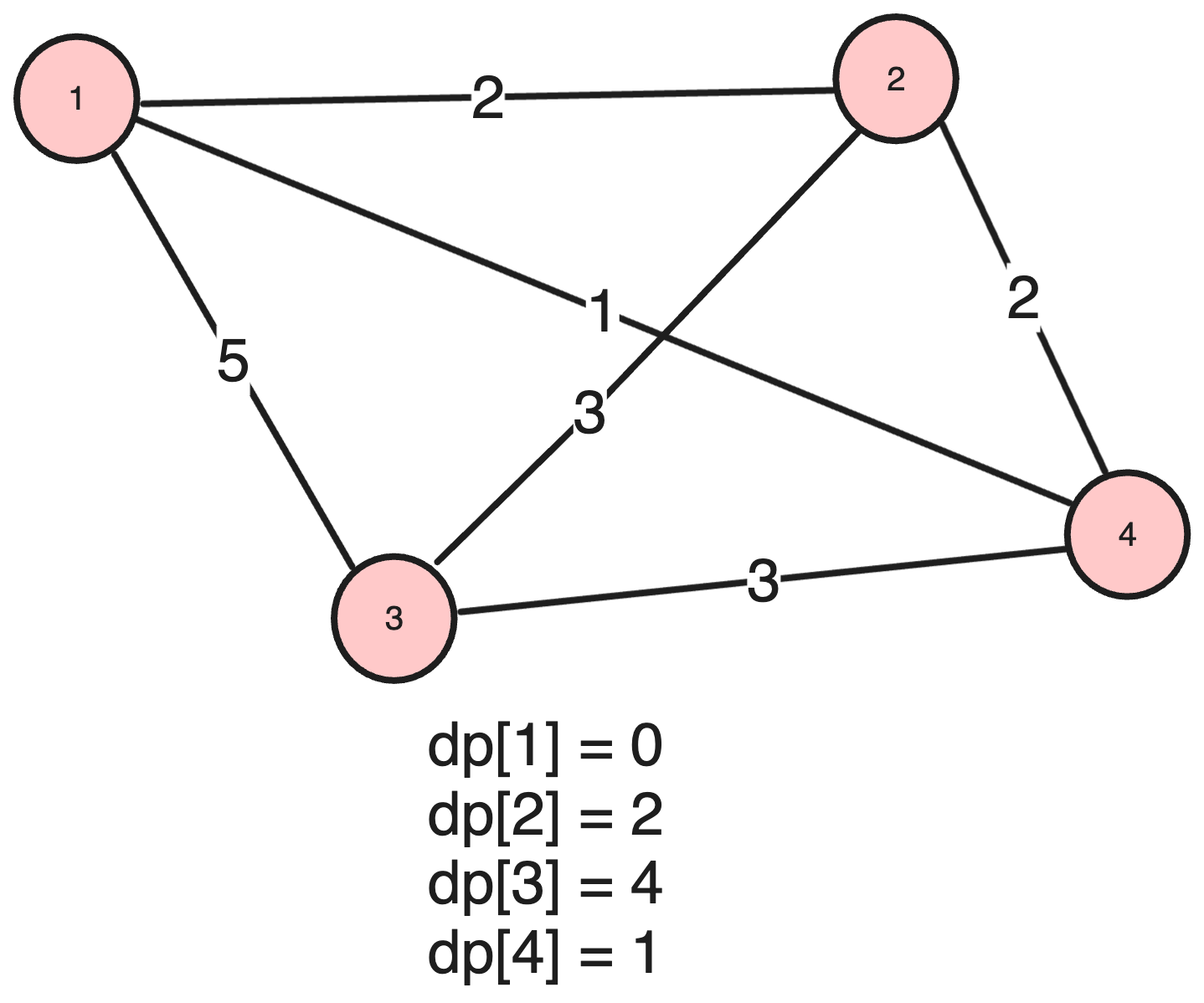
다익스트라 알고리즘 구현 코드
다익스트라 알고리즘을 코드로 구현 시에 큐를 사용하여 연결 노드 중 최단 거리 노드를 구해도 되지만, 최소 힙을 활용하여 구현하는 것이 효율적입니다. 실제로 다익스트라 관련 알고리즘 문제를 풀 때, 큐를 사용할 경우 시간초과가 나는 경우가 대부분입니다(일반 큐로 구현할 경우 간선이 많아지면 시간복잡도가 크게 증가합니다). 파이썬의 경우 heapq를 사용하여 우선순위 큐를 구현하였습니다. 일반 큐를 사용할 경우 시간복잡도는 O(V^2), 최소힙을 사용할 경우 시간복잡도는 O((V + E) log V) 입니다.
# dijkstra
import sys, heapq as hq
def dijkstra(graph, visited, start):
pq = []
dp[start] = 0
hq.heappush(pq, (dp[start], start))
while pq:
value, current = hq.heappop(pq)
visited[current] = 1
for node in range(1, 5):
if graph[current][node] and not visited[node]:
dp[node] = min(dp[node], value + graph[current][node])
hq.heappush(pq, (dp[node], node))
return dp
graph = [[], [0, 0, 2, 5, 1], [0, 2, 0, 3, 2], [0, 5, 3, 0, 3], [0, 1, 2, 3, 0]]
visited = [0] * (5)
dp = [sys.maxsize] * (5)
print(dijkstra(graph, visited, 1))
References
https://chanhuiseok.github.io/posts/algo-50/
https://m.blog.naver.com/ndb796/221234424646
https://maideveloper.com/blog/dijkstras-shortest-path-algorithm
'자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조/알고리즘 이론] 냅색 문제(Knapsack Problem) (2) | 2024.07.24 |
|---|---|
| [자료구조/알고리즘 이론] LCS 알고리즘(Longest Common Subsequence Algorithm) (4) | 2024.07.22 |
| [자료구조/알고리즘 이론] 그리디 알고리즘(Greedy Algorithm) (1) | 2024.07.22 |
| [자료구조/알고리즘 이론] 다이나믹 프로그래밍(Dynamic Programming, DP) (3) | 2024.07.20 |
| [자료구조/알고리즘 이론] 위상 정렬(Topological Sorting) (0) | 2024.07.18 |
