[자료구조/알고리즘 이론] 위상 정렬(Topological Sorting)
위상정렬
위상 정렬이란 방향그래프(Directed Graph)에서 순서가 정해져 있는 작업을 수행할 경우, 순서를 결정하기 위해 사용하는 정렬 알고리즘입니다. O(V+E)의 시간복잡도를 가집니다.
우리가 등교를 위해 옷을 입는 과정을 생각해 봅시다. 셔츠를 먼저 입을 수도, 양말을 먼저 신을 수도, 속옷을 먼저 입을 수도 있지만,
신발을 신고 양말을 신거나 바지를 입고 속옷을 입을 수는 없습니다. 이처럼 순서가 정해져 있는 작업을 수행할 경우 올바른 순서를 도출해 내기 위해 위상정렬을 사용합니다.

위상정렬을 사용하기 위한 조건
- 그래프가 비순환 방향 그래프(DAG: Directed Acyclic Graph)여야 합니다. DAG는 모든 노드에 대해 어떤 노드로부터 다른 노드로의 경로가 유일하며, 다시 출발점으로 돌아오는 경로가 없는 그래프입니다. 그래프에 사이클이 존재할 경우 어떤 순서로 정렬해도 사이클을 끊을 수 없기 때문에 정렬이 불가능합니다.
- 그래프 내의 모든 간선이 방향성을 가져야 합니다.
위상정렬 알고리즘의 종류에는 큐를 이용한 Kahn's Algorithm, DFS를 사용한 위상정렬이 있습니다. 주로 사용되는 방법인 큐를 이용한 Kahn's Algorithm에 대해 알아봅시다.
Kahn's Algorithm(큐를 사용한 위상 정렬)
큐를 활용하는 위상정렬입니다.
알고리즘 과정
1. 진입차수가 0인 정점을 큐에 삽입합니다.
2. 큐에서 정점(정점 A라고 가정합시다)을 꺼내 연결된 모든 간선을 제거합니다.
3. 정점 A에서 연결 간선을 모두 제거한 후에 진입차수가 0인 정점을 큐에 삽입합니다.
4. 위의 과정들을 반복합니다.
- 모든 정점을 반복하기 전에 큐가 비게 되면 사이클이 존재함으로 위상정렬을 적용할 수 없는 그래프입니다.
- 모든 원소 방문 시 큐에서 꺼낸 순서가 위상 정렬의 결과입니다.
아래의 그래프를 Kahn's Algorithm을 사용해서 위상정렬을 수행하겠습니다.
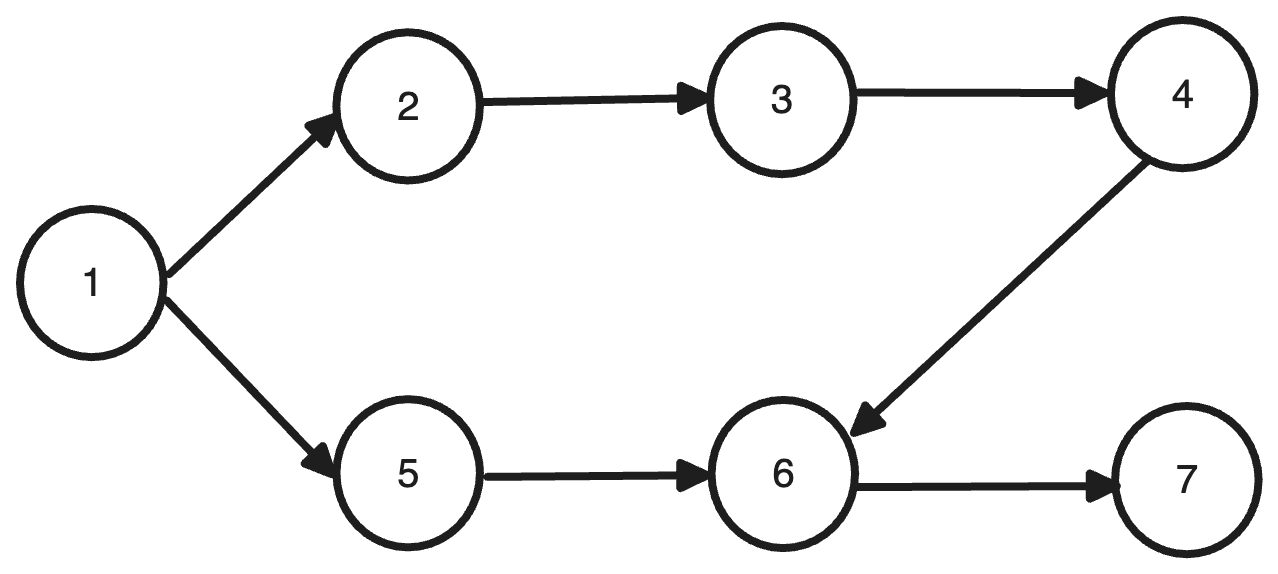
진입차수가 0인 노드 1을 큐에 삽입합니다.

큐에서 1을 꺼내고 1의 연결 간선을 모두 제거 후에 진입차수가 0인 정점을 큐에 삽입합니다.

큐에서 2, 5를 차례로 꺼내고 연결 간선을 모두 제거 후에 진입차수가 0인 정점을 큐에 삽입합니다.

큐에서 3을 꺼내고 연결 간선을 제거 후 진입차수가 0인 정점을 큐에 삽입합니다.
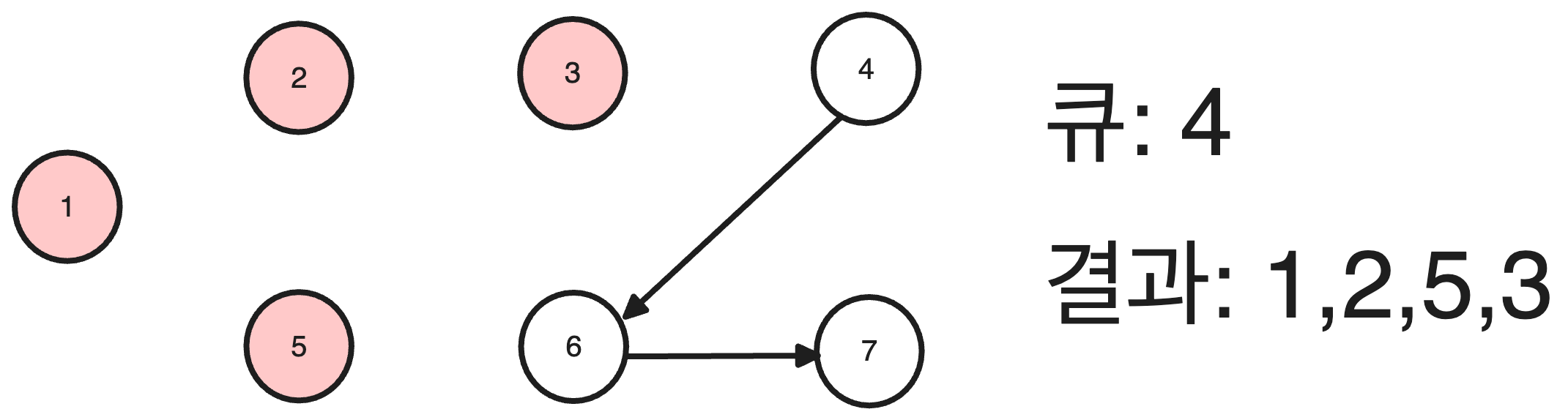
과정을 끝까지 반복할 경우 위상 정렬 결과 값은 1, 2, 5, 3, 4, 6, 7 이 됩니다.
DFS를 사용한 위상 정렬
DFS를 활용하는 위상 정렬입니다.
알고리즘 과정
1. 방문하지 않은 노드(이 노드를 A라고 합시다)를 선택합니다.
2. A를 방문 처리하고 스택에 추가합니다.
3. 스택의 마지막 원소 A의 인접 노드를 스택에 추가합니다. 만약 A와 인접한 노드가 없다면 스택에서 A를 빼고 출력합니다.
4. 스택이 빌 때까지 위의 과정을 반복합니다.
즉 스택에서 삭제되는 순서대로 정렬이 됩니다.
아래의 그래프를 DFS를 활용하여 위상 정렬을 수행하겠습니다.

먼저 임의로 미방문 노드를 하나 선택합니다. H 노드를 시작노드로 선택해 보겠습니다. H 노드를 방문처리하고 스택에 추가합니다.
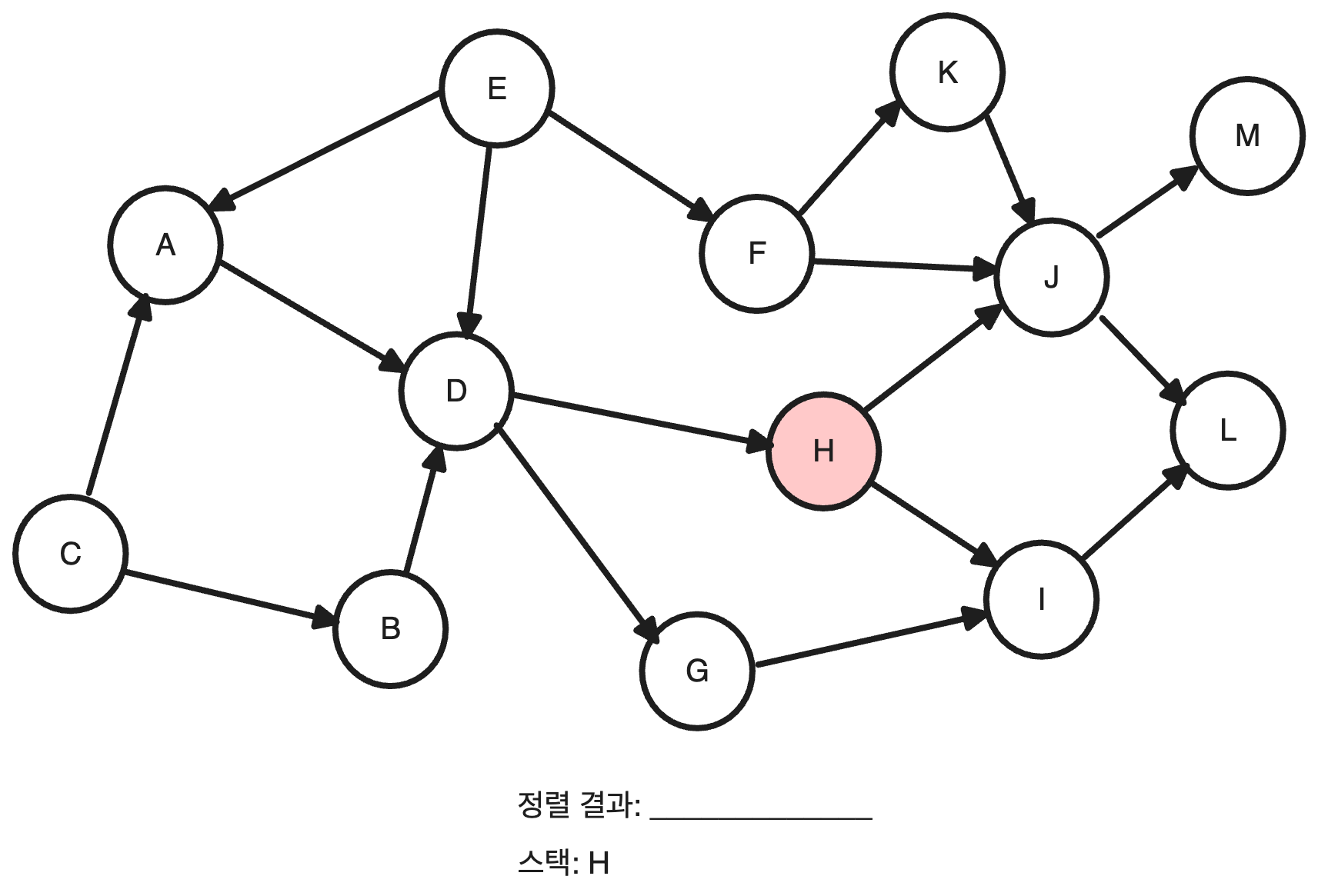
H와 인접한 미방문 노드 중 하나인 J를 방문 처리 후에 스택에 추가합니다. 후에 J와 인접한 노드 M까지 방문 처리와 스택 추가를 진행합니다.

M과 인접한 노드가 없으므로 M을 스택에서 제거해 주고 정렬 결과에 추가합니다. 스택의 마지막 노드인 J와 인접한 노드인 L을 방문 처리 및 스택에 추가합니다.

스택의 마지막 노드인 L과 인접한 노드가 없으므로 L을 스택에서 제거해 주고 정렬 결과에 추가합니다. 후에 J도 마찬가지로 스택에서 제거 및 정렬 결과에 추가합니다.

H와 인접한 노드인 I를 스택에 추가하고 I에게 인접노드가 없기 때문에 스택에서 삭제 후에 정렬해 줍니다. 같은 방식으로 H까지 처리해 주면 결과는 아래와 같습니다.
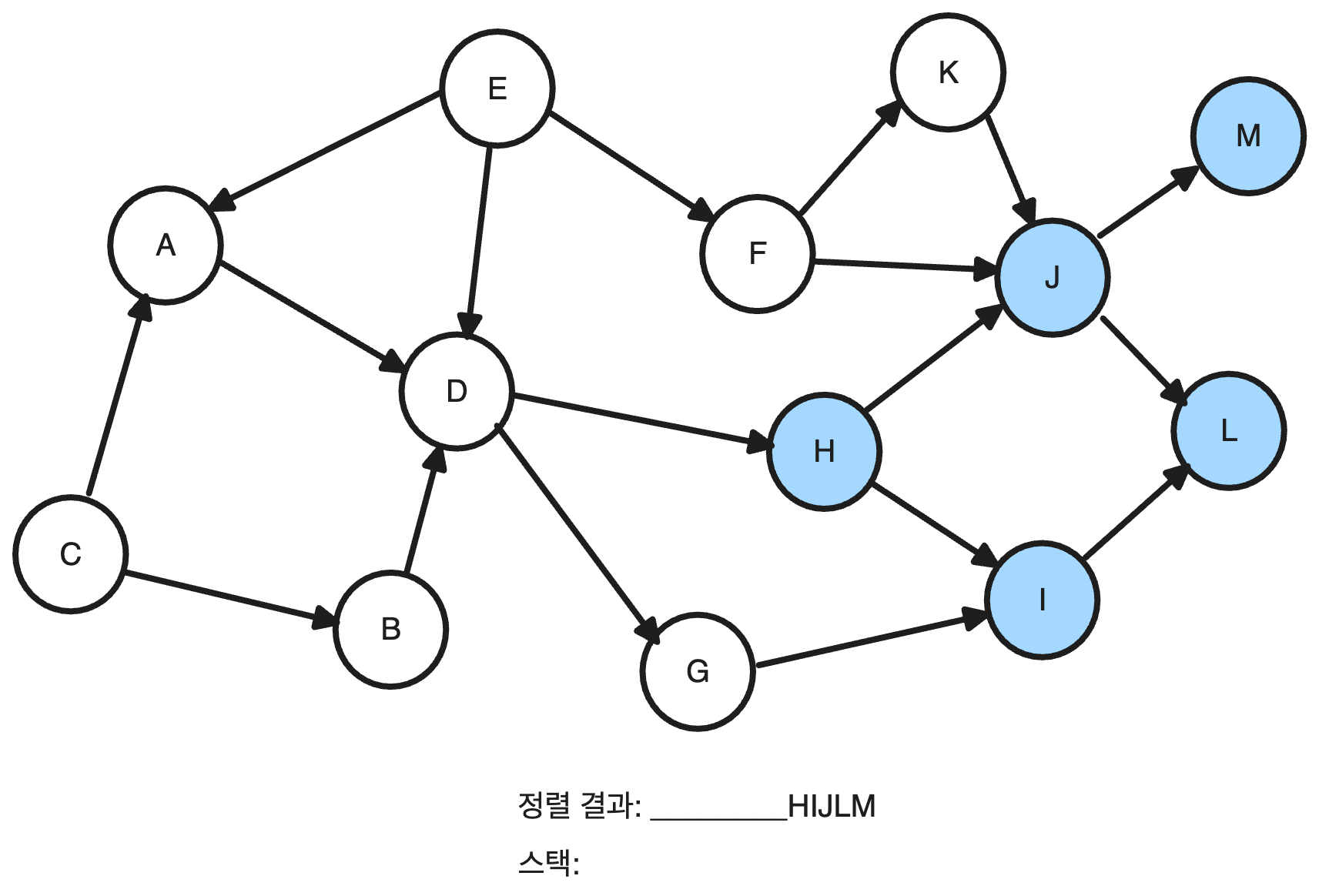
후에 다시 미방문 노드를 선택하여 위의 방식과 같이 진행할 경우 아래의 위상정렬 결과가 나오게 됩니다.

References
https://m.blog.naver.com/ndb796/221236874984
https://www.youtube.com/watch?v=eL-KzMXSXXI&list=LL&index=3&t=1s&ab_channel=WilliamFiset
https://www.youtube.com/watch?v=cIBFEhD77b4&list=LL&index=4&t=35s&ab_channel=WilliamFiset